Network neuroscience and artificial analogues

Introduction

Brain and artificial neural networks are complex, tightly coupled systems whose cognition arises from countless interactions among subcomponents. Consequently, neither are amenable to clean theoretical formulation. Historically neuroscientists have stood by “localizationism,” a coarse framework that attributes brain functions to certain physical regions of the brain. While localizationist models have significantly advanced the state of neuroscience since Paul Broca’s seminal lesion work in 1861, advances in neuroimaging and the availability of “big data” are challenging the assumption that clear anatomical correlates exist for many functional constructs. One recent Stanford study demonstrates that expert-generated proposals for brain region categorization, such as that of the Research Domain Criteria project, do not align with circuits associated with functional domains sourced from some 18,000 papers leveraging fMRI data. It seems that the brain, with its near 100 billion neurons and 1,000 trillion synapses, is best understood in its totality - that is, in terms of the many elements and relationships between its neurobiological systems at all scales. The application of network science to neuroscience is an emerging field known as network neuroscience.

Brain function opacity is mirrored in modern deep learning, which features a strong connectionist philosophy. Deep learning is an intuition-driven, experiment-validated science. Research often consists of hundreds of trials spent searching the architecture and hyperparameter space for a winning final network configuration; little is offered in the way of guarantees over model behavior, performance or complexity. Interpretability techniques can arguably discover what portions of inputs are important to model predictions, but they say little about how the inputs are important to the predictions and what latent representations are developed. Inspection of model internals has, as in neuroscience, been largely localized or conducted under search constraints.

Neuroscience and machine learning frequently exhibit a fault that is the employment of intuitive abstractions which lack correspondence to real-world phenomena. For example, neuroscientific literature has extensively studied a potential frontal lateralization that would vindicate a longstanding theory of emotional valence from psychology. However, fMRI studies have shown that these hemisphere-level models are largely untenable, with responses to positive and negative emotional stimuli relatively distributed. Machine learning researchers similarly suffer from leaky abstractions, often in the form of anthropomorphic projections. Two issues arise when one attempts to map an incoherent cognitive process to a region in a neural network, artificial or otherwise: the cognitive process may be implemented in a distributed fashion over many disparate modules (a “one-to-many” problem); and one module might be involved in many cognitive processes (a “many-to-one” problem). To mitigate these issues, abstractions used to describe network function should be designed from the bottom up.

A network account of the brain is humble. It makes limited assumptions about the involvement of modules in any particular type of computation, accounting for potential long-range dependencies. Studies of networks motivate empirical, rather than theoretical, investigation: rather than constraining search to activity that correlates with preconceived notions of cognition, network science allows arbitrary patterns of computation to emerge that scientists can identify and classify after the fact. Network neuroscience and its artificial analogues augment three domains I’m excited about:

1. Interpretation: explaining and predicting the behavior of networks with network analysis.
2. Generation: developing models that generate synthetic networks which can be used for simulation or downstream tasks.
3. Control: leveraging a fine-grained understanding of the influence of certain nodes and edges to perturb or manipulate networks for specific purposes.

I am especially interested in the synthesis of network approaches across neuroscience and machine learning since it appears that existing research in both fields is ripe for transfer. Because the brain and artificial neural networks are differentially amenable to different types of network analysis, I anticipate that future insights in one field may accelerate progress in the other.

Interpretation

Modeling relationships between components in a network aids understanding of the computation of the network and predicts external properties. For instance, neuroscientists may be able to more accurately characterize diseases and their symptoms as well as predict their onset in early stages by assessing certain graph-theoretic metrics. Network neuroscience borrows from topological data analysis in addition to graph theory; for instance, by translating data into simplicial complexes and computing persistent homology.

Schizophrenia is one disease that cannot be understood without a picture of whole-brain functional connectivity. One can build functional connectomes by observing statistical association between the time series of nodes in a brain network, typically anatomically defined regions of interest (ROIs). These time series derive from resting-state or task-based functional magnetic resonance imaging (fMRI) studies that measure the activity of the ROIs over a scanning period. In the construction of the connectome, nodes are the ROIs and edges represent the strength of connectivity between a pair of nodes. This strength can be measured with metrics such as correlation, partial correlation, Granger causality, or transfer entropy. Liu et al. show that the functional networks of schizophrenic individuals have reduced “small-worldness” compared to healthy individuals, meaning that the normal efficient topological structure with high local clustering is disturbed: absolute path length increases and clustering coefficients decrease. Schizophrenic individuals additionally exhibit significantly lower connectivity strength, i.e. the mean of all pairwise correlations in the functional connectome, which potentially explains patients’ impaired verbal fluency in terms of reduced processing speed.

Networks can be analyzed at different scales and of different types. Integrating neurobiological networks at the micro- and macro-level can help us understand the full path from genetic factors to brain connectivity to behavior. For example, joint analyses of brain and social networks have shown that an individual’s functional connectivity patterns predict aspects of ego-network structure. Multilayer networks - networks involving different edge types with each edge type encoded in a separate layer - can capture temporal interdependencies or combine information from complementary imaging modalities. The study of network dynamics, i.e. how functional networks emerge over fixed anatomical networks, may help neuroscientists and machine learning researchers alike understand the importance of structural priors. Structure-function coupling, the ability of anatomical connectivity to predict the strength of functional connectivity, is supposed to reflect the functional specialization of cortical region. Indeed, the specialized and evolutionarily conserved somatosensory cortex exhibits strong coupling while highly expanded transmodal areas exhibit weak coupling, supporting cognitive flexibility. Structure-function relationships bear on developmental psychology: significant age-related increases in structure-function coupling are observed in the association cortex, while age-related decreases in coupling are observed in the sensorimotor cortex. These results signal the development of white matter architecture throughout adolescence to support more complex cognitive capabilities. Variable emergence of coupling may explain intraindividual variance in children’s learning patterns.

Techniques from network neuroscience have the potential to improve machine learning researchers’ understanding of artificial neural networks. OpenAI’s interpretability team kicked off a research agenda in 2020 studying subgraphs in neural networks that purportedly implement meaningful algorithms, such as curve detection in visual processing. These subgraphs are called circuits. They ingest, integrate, and transform features, propagating information along weights between neurons. Unlike neuroscience, machine learning interpretability benefits from having the entire neural connectome available. Simply having a full anatomical connectome, however, is not enough to understand underlying computation. “Could a Neuroscientist Understand a Microprocessor?” uses traditional neuroscientific techniques, such as analyses of anatomical connectomes and tuning curves, to reverse-engineer a microprocessor. The authors point out that without a clear map from anatomy to function, circuit motifs are meaningless. The same could be said for circuit motifs in artificial neural networks. OpenAI’s circuit work attempts to ascribe function to circuits by interpreting feature visualizations, dataset examples, and conducting other analyses. This requires human labor and does not seem scalable in the long run. The application of functional connectomics and structure-function relationship analysis to neural networks is a viable solution. One work investigates topological differences in Trojaned and clean deep neural networks by comparison of persistence diagrams, showing that Trojaned models have significantly smaller average death of the 0D homology class and maximum persistence of the 1D homology class.

Graph neural networks (GNNs) may be natural tools for the study of biological and artificial neural networks because they take graphs as input. Over several layers, each node updates its representation as a function of its neighbors. The GNN uses final node representations to make node-level, edge-level, or graph-level predictions. One could train a GNN over a functional connectome, for instance, to predict whether or not a patient has depression; or possibly over many artificial neural networks to detect universal circuits. BrainGNN is one instance of a GNN used for fMRI analysis. Its graph convolutional layers implicitly assign ROIs to communities to compute weight matrices, discovering interpretable task-related brain community structure. Its ROI pooling layers retain only the most salient ROIs for the predictive task, automatically finding biomarkers. (Check out a beginner-friendly tutorial by my friends and I in which we implement cGCN, a GNN for fMRI analysis.)

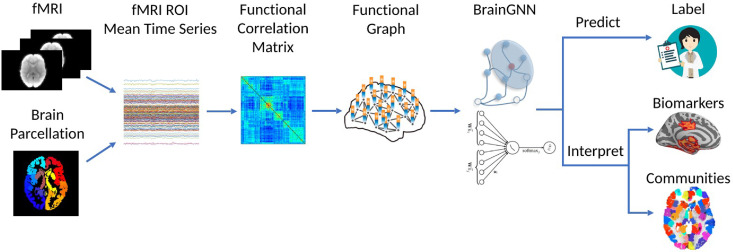
BrainGNN pipeline.

Generation

Generative models compress statistically regular network topologies to create synthetic networks. They use wiring rules or structural constraints to build neurobiologically plausible models. For example, Watts and Strogatz’s seminal “Collective dynamics of ‘small-world’ networks” randomly rewires edges in a ring lattice to create networks exhibiting the small-worldness property previously discussed. These sorts of models hypothesize mechanistic sources of certain real-world network phenomena, such as long-tailedness, and are easily comparable with real-world networks for verification. Generative models can be used to simulate diseases, or facilitate in silico experiments where scientists attempt to steer trajectories of neural circuitry. In turn, the construction of synthetic biological networks can inform machine learning researchers’ architectural design and selection.

The pairwise maximum entropy model has proven to be one simple but powerful model for inferring functional network topology from structural network topology and vice versa. This method defines a probability distribution over the 2^N possible states for N neurons, since neurons either spike or remain silent. To measure the effectiveness of a pairwise description of a functional network, the model computes the reduction in entropy from a distribution given only first-order correlations to second-order correlations to the total reduction in entropy given network correlations at all orders, or the multi-information. An early study demonstrated that maximum entropy models could capture 90% of multi-information for various cell populations. Later, this model was used to accurately and robustly fit BOLD signals in resting-state human brain networks.

Synthetic networks fit to brain networks can serve as bioinspiration for practical artificial neural networks, potentially reducing parameters and increasing interpretability. Spatial neural networks follow generative neurobiological models that impose costs for long connections between neurons, encouraging efficient grouping. Neurons are assigned two-dimensional learned spatial features. Each layer receives a penalty that is the sum of the spatial distances between that layers’ nodes and the neurons to which they are connected. The authors train the spatial network on two relatively independent classification tasks, MNIST and FashionMNIST. They find that two subnetworks emerge, one for each task, that perform only slightly worse on each task than the full network. By comparison, split full-connected networks perform considerably worse. Pushing neural networks towards such modularity may be helpful for human interpretation and explanation. Conversely, artificial neural networks are useful for interpreting and building synthetic biological neural networks; while not explicitly designed to simulate biological neural networks, similar features can and do emerge. Researchers have found that layers in convolutional neural networks (CNNs) can predict responses of corresponding layers in the higher visual cortex, demonstrating the importance of hierarchical processing. The CNNs thus serve as generative models for neuronal site activity.

Neural architecture search, which strongly overlaps with the field of meta-learning, looks for optimal neural network topologies. Hypernetworks can aid neural architecture search by generating weights for a given architecture, an alternative to training neural networks from scratch. Classically hypernetworks have used 3D tensor encoding schemes or string serializations to map from architectures to weights. These fail to explicitly model architecture network topology, so Zhang et al. construct graph hypernetworks (GHNs). GHNs learn a GNN over neural architectures represented as computation graphs, generating weights for each node with a multilayer perceptron given that node’s final embedding. Performance with generated weights are well-correlated with final performance. Architectures with weights generated by GHNs achieve remarkably high prediction accuracy, with some at 77% on CIFAR-10 and others at 48% top-5 accuracy on ImageNet.

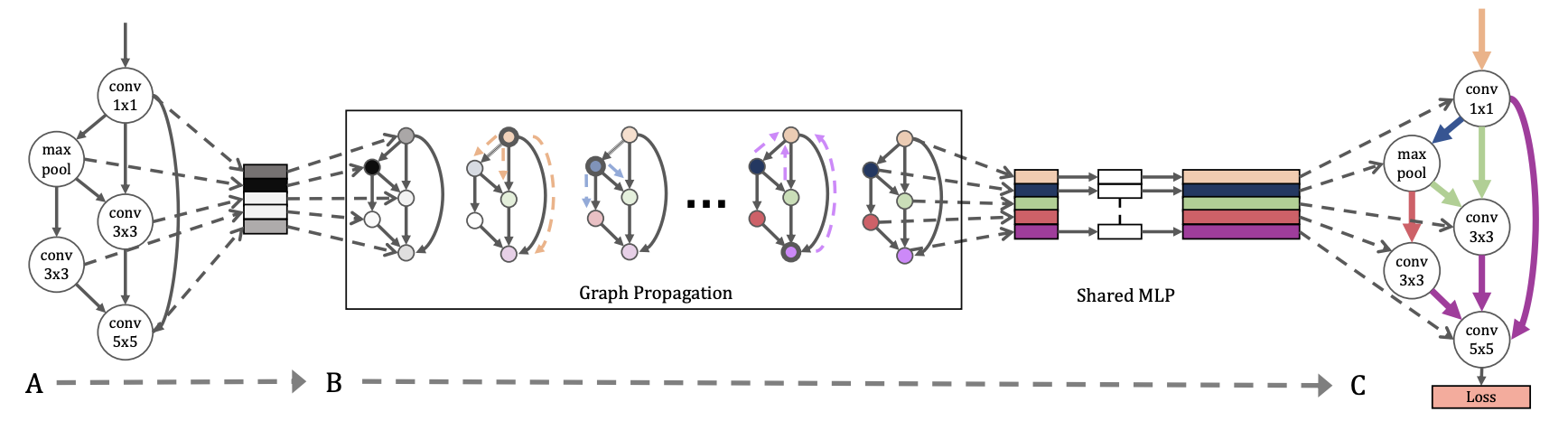
Generating weights with a GHN.

Deep generative models of graphs, similar to GHNs, can be used to model artificial neural networks and biological neural networks alike. Typically generative models in network neuroscience use hand-designed wiring rules, which is helpful for the interpretation of network properties that emerge as a result of these rules. However, they may lack fidelity and scale poorly to complex topologies that are not human-interpretable. Deep generative models allow for topological constraints to be learned instead and produce graphs faithful to empirical networks. GraphRNN is one such example, an autoregressive model that iteratively adds nodes to a graph and predicts edges to previous nodes. GNNs are also useful for generation since they learn rich structural information from observed graphs; Li et al. condition on GNN-produced graph representations to determine whether or not to add nodes or edges. The application of these methods to brain networks, structural or otherwise, appears relatively unexplored.

Control

Beyond diagnoses, the modeling of brain networks and the generation of synthetic networks serve the cause of goal-directed network manipulation. Network manipulation is important for safely conducting disease intervention, building brain-computer interfaces, and developing neuroprosthetics. Exogenous inputs to neural systems include lesions, brain stimulation, and task priming.

The intersection of network control theory and neuroscience has proved useful. Yan et al. applied network control principles to C. elegans, annotating brain states at certain time steps as linear dynamical systems by adding adjacency-matrix-selected previous states of nodes to the effects of stimuli, such as anterior gentle touch, applied to receptor neurons. The cells to be controlled were predicted to be controllable if, with sufficient stimuli, the states of those cells could reach any position in the state space. These control principles were able to predict which neurons were critical in the worms’ response to gentle touch, because their ablation resulted in a decrease in the number of independently controllable cells. Similar processes can be conducted in human connectomes: Gu et al. construct from diffusion spectrum imaging data a controllability Gramian, a matrix whose eigenvalues and structure signal the magnitude and selection of control areas that may optimize cognitive function. The Gramian indicates that the human brain is theoretically, but not easily, globally controllable via a single brain region. While highly connected regions are able to move the brain to easily reachable states, weakly connected regions critically move the brain into difficult-to-reach states, such as high performance states as measured by IQ. These results challenge notions that only well-connected hubs should be targets for intervention, painting a more nuanced view of network controllability. Control-theoretic approaches in the neuroscience community could be used in machine learning work on model editing and controllable outputs, and appear as of yet uninvestigated.

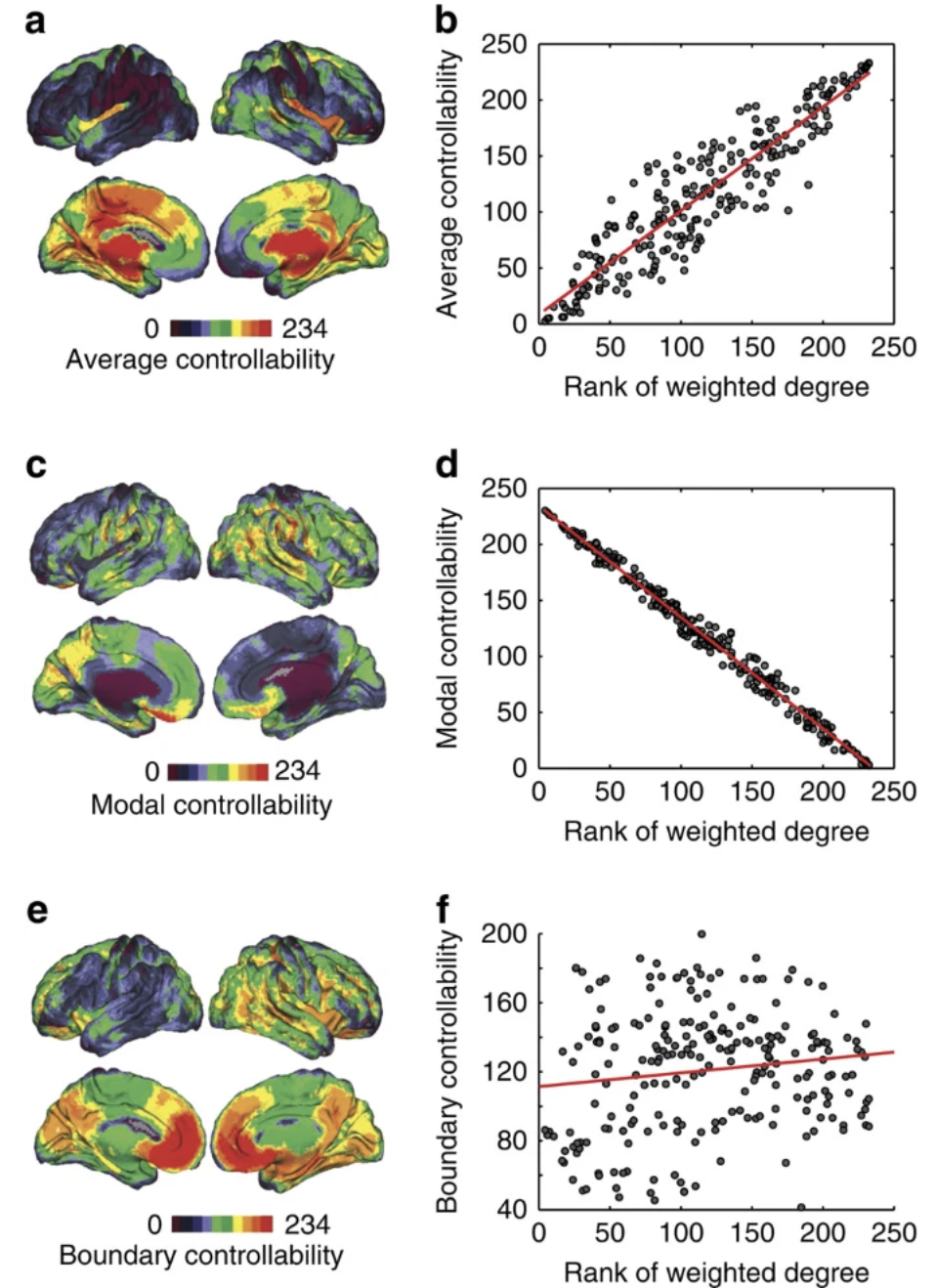
Average controllability is correlated with node degree. Modal controllability (ability to move brain into difficult-to-reach states) is anticorrelated with node degree. Boundary controllability (ability to couple or decouple different cognitive systems) is not strongly correlated or anticorrelated with node degree.

Some work has attempted to track information flow across artificial neural networks with the motivation of reducing undesirable biases, as well as serve as test grounds for reward circuit manipulation in the brain. Pruning edges with high mutual information with a message, such as a protected attribute, produce larger reductions in bias at the output. These edges are therefore potential targets for intervention. Neuroscientific experiments may mirror this approach to narrow down neural targets for optogenetic stimulation. Additionally, feature attribution methods used to explain machine learning models, such as integrated gradients, could be employed by neuroscientists to identify computation-relevant sites in the brain. Integrated gradients attribute predictions of machine learning models to input features by calculating gradients of output with respect to features of input along an integral path. One could imagine analogously applying a stimulus to various target sites in a biological neural network and scaling the magnitude of this stimulus to calculate an integrated gradient, thus attributing the activity of another region in the network to the target site.

Instead of performing manual inspection, there is room to use deep learning, e.g. GNNs, to predict the effect of a perturbation on a biological or artificial neural network. One could use synthetic biological networks to simulate trajectories away from maladaptive network topologies. Or in GNN inference, machine learning engineers could occlude or alter certain subgraphs in brain networks and observe effects on predictions. For instance, changing the value of a feature of an ROI might cause a GNN to predict that a diseased brain is now healthy. Temporal Graph Networks, which assign memory states to nodes, could predict new functional or structural edges in brain networks based on past activities. One could ablate a portion of a biological or artificial neural network and observe the difference in the evolution of that network over time. Such a study could confer greater insight into the mechanisms underlying neuroplasticity, or the recovery of ablated artificial neural networks.

Conclusion

Network science offers an integrative perspective on artificial and biological neural networks. Empirical investigation and computational modeling of the activity of not only localized regions, but their multitudinous spatiotemporal interactions, capture the hierarchical and distributed computation that lend the brain and machine learning models their efficiency and great expressive power. Bridging network science-inspired methods in artificial intelligence and neuroscience may unlock powerful insights as well as establish a common lingo to enable interdisciplinary synthesis.